The understanding of algebra is one of the keys to succeeding in higher level math courses. For this reason we must find a way to help more students become competent in algebra. I have mentioned in previous articles that I taught algebra to 8th graders in an urban middle school. I repeat it here so that you understand how well the activity I am describing helped my students easily grasp the graphing of lines and parabolas on the coordinate plane. The Algebra Walk is a true gem of an activity.
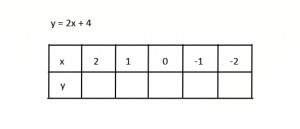
Prior to the algebra walk (aka human graphing) we had spent time using input-output tables with a variety of equations. This activity allowed the students to become comfortable working with ordered pairs. Here is an example of an input-output table that we used.
I also introduced T-tables for those who found them easier to use.
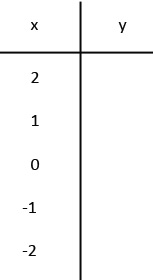
y = 2x+4
After the students are comfortable with the tables it is time to start the algebra walk.
Provide your students with the three equations you will use for the activity the day before you are going to do this. Have them produce the input-output tables for these equations as homework with a range of numbers from 4 to -4. These answers can be self checked when you do the activity. Also provide graph paper to be used during the actual activity. Prepare 3 x 5 cards with ordered pairs that match the equations from the homework assignment. I used one linear equation with a positive co-efficient, another with a negative co-efficient and finally one that would produce a parabola.
The next part of the preparation will depend on the amount of space you have in your classroom, in a nearby area in the school, or even just outside of the building. I was fortunate enough to have a supportive environment so that I could use an open tiled area and set up an x-y axis using masking tape. If you aren’t this fortunate you can purchase a clothesline (yes they still exist) and designate one part as the x axis and the other the y axis. Tie knots at one foot intervals to mark off the numbers on the line. Use a marker to color over the knots that will represent the origin so it is easily found. You are now ready to “walk the graph”.
When I used this activity I had at least 5 inclusion students so I always had a few calculators with me (even if I knew they weren’t needed) for anyone who wasn’t quick at computation. For the most part they were not used and simply acted as a security blanket.
Each equation was handled in the same way, so simply repeat the following steps for each one.
1. Place your x-y axis in the area that you will use.
2. Hand 9 students the ordered pair cards and have them line up on the x axis. The remainder of the class will check their input-output answers as the students with the ordered pairs move from the x axis to their designated ordered pair. Once the line or parabola was created by the human graphers the other students would duplicate what they saw on their graph paper.
Repeat with 9 different students for each of the other equations.
By the time the class is finished they will have 3 input-output tables, 3 equations, and 3 graphs. Return to the classroom and discuss what the students noticed. Finish with each student writing about their experience and what they learned.
Homework that day was to complete the input-output tables and the graphs for 3 new problems.
For in class reinforcement, I used large graph paper and graphed the 3 algebra walk problems so that they would be visible on the bulletin board for those who needed a reference.
I found this activity to be the best introduction to graphing that I had ever used. Most of my students were comfortable graphing equations within a few days of completing this activity.
What I liked the most about the algebra walk is that it included auditory, visual and kinesthetic components to reach the most students possible.



